고전입니다.
NeurIPS 2017에서 발표된 NLP 논문으로, Transformer로 잘 알려진 Attention Is All You Need입니다.
https://arxiv.org/abs/1706.03762
Attention Is All You Need
The dominant sequence transduction models are based on complex recurrent or convolutional neural networks in an encoder-decoder configuration. The best performing models also connect the encoder and decoder through an attention mechanism. We propose a new
arxiv.org
1. Introduction
RNN, LSTM 등의 모델들은 sequence modeling분야(언어 모델링, 기계 번역 등)에서 대표적으로 사용되던 모델입니다.
RNN(Recurrent Neural Network) 모델은 입력값과 출력값의 문자(기호) 위치를 기반으로 계산을 수행합니다. 이전 단계의 은닉 상태(hidden state) $h_{t-1}$와 현재 단계의 입력값 위치 t가 주어지면 현재 단계의 은닉 상태 $h_t$를 생성하는 식입니다. 보다시피 이 방법은 순차적인 성질을 띠고 있어서, 하나의 sample에 대해 병렬계산을 할 수 없습니다. 때문에, 입력 문자열이 길어질 수록 메모리 한계 때문에 계산 수행이 어려워진다는 문제점이 있습니다. 이를 극복하기 위한 다양한 연구가 수행되었지만, 여전히 근본적인 문제는 해결되지 않은 상태입니다.
Attention 매커니즘은 sequence modeling과 변환 모델에서 핵심적인 요소가 되었습니다. Attention은 입력값 또는 출력값 문자열의 단어간 거리와 관계 없이 두 단어간의 의존성을 모델링할 수 있다는 장점이 있습니다. 대부분의 기존 모델들은 Attention을 RNN와 함께 사용하고 있었습니다.
본 연구에서는 RNN을 전혀 사용하지 않고 온전히 Attention만 사용한 모델구조인 Transformer를 선보입니다. Transformer는 유의미한 병렬계산을 수행할 수 있으며, 번역 작업에 있어서 새로운 SoTA 성능을 보였습니다.
2. Background
계산량을 줄이려는 시도를 한 사례는 Extended Neural GPU, ByteNet, ConvS2S 등이 있습니다. 이들은 모두 CNN을 이용하여 입력값과 출력값 위치를 병렬적으로 계산하였습니다. 하지만 CNN도 결국 두 단어 간의 거리가 멀어질 수록 계산량이 늘어나는 단점을 보완할 수 없었습니다(ConvS2S에서는 선형적으로, ByteNet에서는 로그로). 하지만 Transformer에서는 그 계산량은 항상 상수로 고정됩니다. 여러 위치의 정보를 평균적으로(attention-weighted sum) 반영하는 Attention 특성상 정보의 해상도(정밀도)가 낮아진다는 단점이 있지만, 이는 3.2절에서 언급할 Multi-Head Attetion으로 보완할 수 있습니다.
Self-attention(intra-attention)은 하나의 sequence에서 서로 다른 위치를 관계 짓는 매커니즘입니다. 이는 지문 이해, 요약 등 다양한 작업에서 성공적으로 사용되고 있는 매커니즘입니다.
End-to-end memory network는 sequence-aligned recurrent 대신 recurrent attention 매커니즘을 사용하며, 간단한 문답이나 language modeling 작업에 좋은 성능을 보였습니다.
Transformer는 sequence-aligned RNN 이나 CNN을 사용하지 않고 오직 self-attention만을 사용한 최초의 사례입니다.
3. Model Architecture
대부분의 뛰어난 sequence 변환 모델은 encoder-decoder 구조를 가지고 있습니다. 여기서도 encoder는 입력 sequence $\mathbb{x} = (x_1, ... , x_n)$를 연속적인 값 $\mathbb{z} = (z_1, ... , z_n)$로 변환하며, decoder는 $\mathbb{z}$를 기반으로 출력 sequence $\mathbb{y} = (y_1, ... , y_m)$ 를 생성합니다.
$\mathbb{x} = (x_1, ... , x_n) \rightarrow \mathbb{z} = (z_1, ... , z_n) \rightarrow \mathbb{y} = (y_1, ... , y_m)$
각 단계는 이전 단계들의 값들을 기반으로 현재 단계를 추론하는 auto-regressive 방식으로 동작합니다. Transformer는 stacked self-attention과 point-wise 완전연결 계층을 이용해 이 구조를 구현하였습니다.
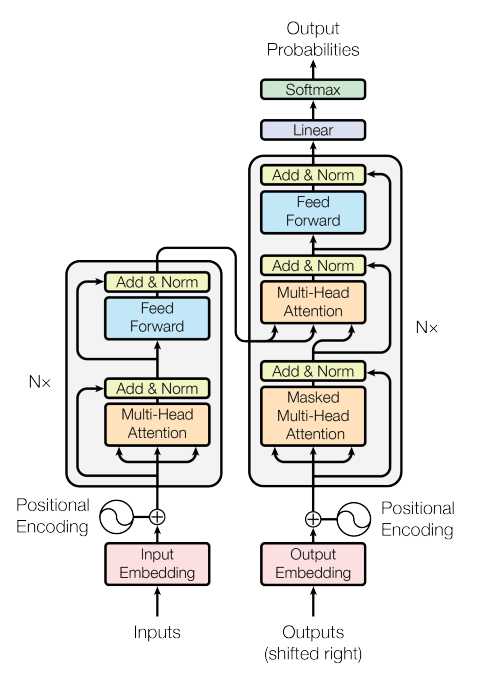
3.1. Encoder and Decoder Stacks
3.1.1. Encoder
Encoder는 6개의 동일한 계층들로 이루어져 있습니다([그림 1]에서 N = 6). 각 계층은 다시 2개의 하위 계층(multi-head self-attention, position-wise fully connected feed-forward)으로 이루어져 있습니다. 각 계층은 residual connection*이 적용되어 다음과 같이 계산됩니다. 모든 하위 계층들은 $d_{model}=512$차원의 값을 가지도록 합니다.
$\text{LayerNorm}(x + \text{Sublayer}(x))$
* Residual connection : 딥러닝 네트워크에서 입력값을 변형 없이 출력에 더해주는 구조
3.1.2. Decoder
Decoder도 마찬가지로 6개의 동일한 계층으로 이루어져 있으나, 각 계층은 encoder의 2개 하위 계층에 multi-head attention을 하나 더 추가하여 3개의 하위 계층으로 이루어집니다. 추가된 multi-head attention은 encoder의 출력값을 입력값으로 가집니다. 첫 번째 attention은 masking을 적용했는데, 이를 통해 decoder가 현재 위치 이후 미래의 sequence값을 참초하지 못하게 합니다. 미래의 값을 미리 알면 안 되기 때문입니다.
3.2. Attention
Attention 함수는 query와 (key-value) 짝을 출력값으로 변환하는 작업을 수행합니다(qurey, key, value, 출력값은 모두 벡터). 출력값은 각 value에 대한 가중치 합으로 계산되며, 여기서 가중치는 query가 각 key와 얼마나 관련 있는지 판단하는 compatibility function으로 계산됩니다.
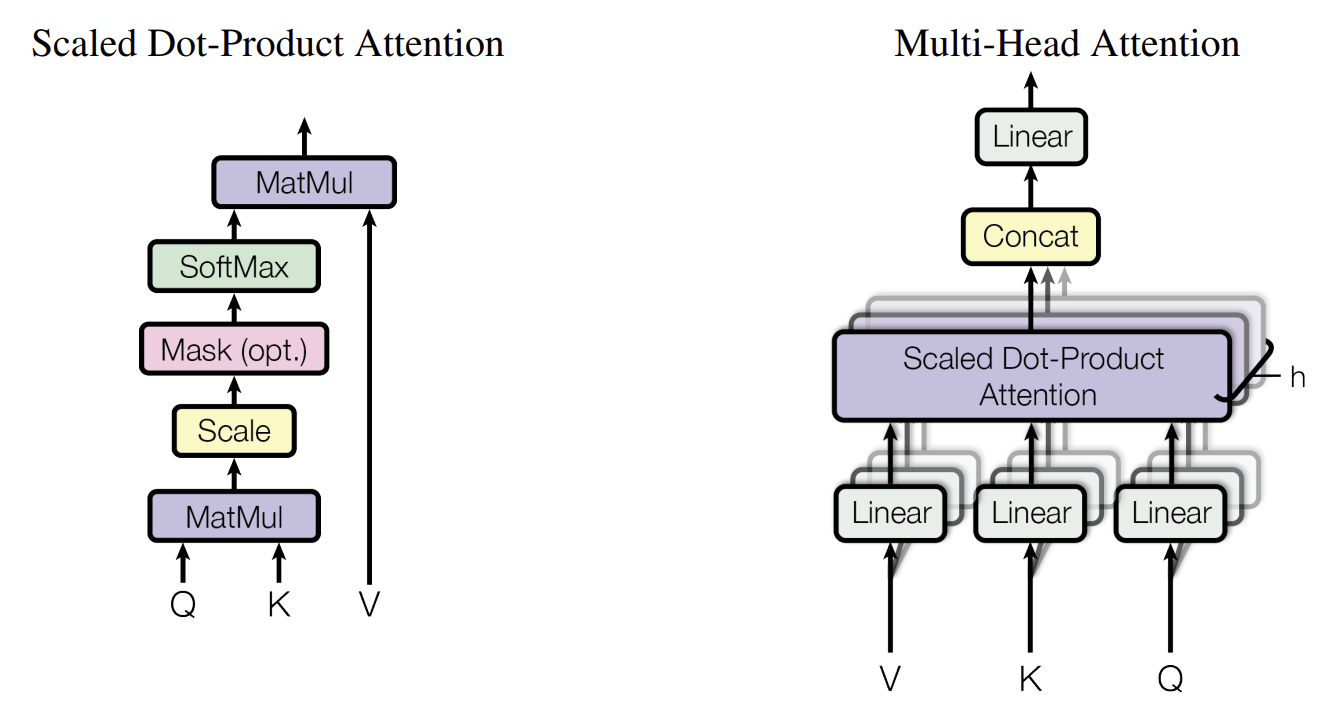
3.2.1. Scaled Dot-Product Attention
Attention의 입력값으로는 아래 세 가지를 받습니다.
| 차원 | 의미 (각 위치는~) | 예시 ('I have a cat' 에서 'cat'은~) | |
| Query | $Q \in \mathbb{R}^{N \times d_k}$ | 어떤 값을 찾아야 하는가? | 주어가 무엇인지 찾아야 한다. |
| Keys | $K \in \mathbb{R}^{N \times d_k}$ | 어떤 특징을 가지는가? | 목적어이므로, 서술어의 목적이 될 수 있다. |
| Values | $V \in \mathbb{R}^{N \times d_v}$ | 어떤 값을 가지는가? | 'cat'을 나타내는 값 |
이에 대해 다음 단계의 연산을 거칩니다.
| 단계 | 수식 | 의미 | 왜? | 출력 차원 |
| 1 | $Q^TK$ | 유사도 계산 | 벡터 내적 계산은 두 벡터의 방향이 가까울수록 값이 커짐 | $\mathbb{R}^{N \times N}$ |
| 2 | $\cdot / \sqrt{d_k}$ | 분산 정규화 | $Q^TK$의 분산은 $d_k$이므로 차원 $d_k$가 커지면 분산도 증가함. 분산이 증가하면 결과값도 커지고, 이는 softmax 결과값이 지나치게 튀게 만들어 기울기 소실을 유발할 수 있음. 따라서 표준편차인 $\sqrt{d_k}$로 나누어 분산을 정규화 시킴 |
$\mathbb{R}^{N \times N}$ |
| 3 | softmax($\cdot$) | 정규화 | 0 ~ 1 사이의 값을 가지도록 가중치값 정규화 | $\mathbb{R}^{N \times N}$ |
| 4 | $\cdot V$ | 가중치 연산 | 가중치와 V값 계산 | $\mathbb{R}^{N \times d_v}$ |
따라서 다음과 같이 나타낼 수 있습니다.
$\text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V \quad (1)$
위 식은 dot-product attention을 기반으로 만들어졌습니다(2번 과정이 추가되었습니다). 이것 말고도 additive attention이라는 기법도 있는데, 둘을 비교했을 때 전자가 더 효율적이라고 합니다. 행렬 곱셈 자체를 최적화하여 구현할 수 있기 때문입니다.
3.2.2. Multi-Head Attention
이 절에서는 먼저 $d_{model}$ 차원의 입력값을 3.2.1.절에서 사용한 Q, K, V 값의 형태로 변환하는 연산을 소개합니다. 선형 사형(linear projection)을 이용하면 차원을 바꿀 수 있으며 아래 사영 행렬을 사용합니다.
$W^Q \in \mathbb{R}^{d_{model} \times d_k} \quad W^K \in \mathbb{R}^{d_{model} \times d_k} \quad W^Q \in \mathbb{R}^{d_{model} \times d_v}$
또한 본 연구에서는 $d_{model}$차원 상의 값 한 가지 보다 여러 값들에 대해 수행하는 것이 더 효과적이라고 합니다. 총 h번(=head가 h개)의 attention 연산은 h개의 $d_v$차원의 출력값을 내놓게 되며, 이를 합쳐 다시 전체 출력 차원에 맞게 사영하면 연산이 완료됩니다(그림 2).
$\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, ..., \text{head}_h)W^O \quad where$
$\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V), \quad W_i^O \in \mathbb{R}^{hd_v \times d_{model}}$
본 연구에서는 $h=8$로 두었고, $d_k = d_v = d_{model} / h = 64$로 두었습니다. 각 head의 차원 값들이 줄어든 만큼, 총 계산량 또한 차원 축소를 하지 않았을 때의 single-head attention의 계산량과 비슷해집니다.
3.2.3. Applications of Attention in our Model
Transformer에서 multi-head attention을 사용한 부분은 아래 세 가지 경우 입니다.
- Encoder-decoder attention(Cross-Attention) 계층([그림 1]에서 decoder 두 번째 계층) : query는 이전의 decoder 계층에서 오며, key와 value는 encoder에서 옵니다. 이는 decoder가 seqence의 모든 위치를 참조하도록 합니다.
- Encoder의 self-attention 계층 : 이전 encoder 계층의 출력값(Z)을 입력으로 받으며, encoder가 이전 계층 encoder의 모든 위치를 참조하도록 합니다.
- Decoder의 self-attention 계층 : 이전 decoder 계층의 출력값(Y)을 입력으로 받으며, masking을 통해 이전 계층 decoder의 값 중 자신의 위치 이전의 모든 부분을 참조하도록 합니다.
3.3. Position-wise Feed-Forward Networks
Fully connected Feed-Forward Network(FFN)는 각 위치별로 따로 적용됩니다(연산은 모두 동일합니다). 이 신경망은 두 개의 선형 변환과 ReLU 활성화 함수로 구성되어 있습니다.
$FFN(x) = max(0, xW_1 + b_1)W_2 + b_2 \quad (2)$
각 위치별로 연산식은 모두 같지만, 가중치 $W$는 계층마다 다릅니다.
3.4. Embeddings and Softmax
입력값과 출력값 token을 $d_{model}$차원의 벡터로 변환하기 위해 학습된 embedding 값을 사용합니다. 또한 decoder의 출력값을 다음 token 확률로 변환할 때 학습된 선형변환계층과 softmax를 사용합니다. 이 embedding 계층과 선형변환계층은 같은 가중치를 사용합니다(단, embedding 계층에서는 $\sqrt{d_{model}}$을 따로 곱해줍니다).
3.5. Positional Encoding
Transformer는 재귀나 합성곱 없이 attention만 있기 때문에, 어떻게든 token들의 위치에 대한 정보를 넣어주어야 합니다. 때문에 "positional encoding"이라고 하는 $d_{model}$차원 값을 embedding 값에 더해주는 단계가 존재합니다 (embedding 값과 같은 차원을 가지므로, 더할 수 있습니다).
본 연구에서는 서로 다른 진동수의 사인 / 코사인 함수를 positional encoding으로 사용했습니다.
$PE_{pos, 2i} = sin(pos/10000^{2i/d_{model}})$
$PE_{pos, 2i+1} = cos(pos/10000^{2i/d_{model}})$
$pos$는 위치, $i$는 차원 크기입니다.
4. Why Self-Attention
이 절에서는 self-attention 계층층을 재귀나 합성곱 계층과 비교하여 분석합니다. 평가 항목으로는 아래 세 가지를 고려하였습니다.
- 계층별 복잡도
- 병렬화 가능한 연산량. 순차적으로 연산하는 최소 연산량으로 측정했습니다.
- 최대 경로 길이. 거리가 먼 의존성을 학습할 때는 경로가 짧을 수록 학습하기가 쉬워집니다.

[표 1]에서 보듯, self-attention은 위치와 관계 없이 순차적 연산을 상수 시간 내에 수행할 수 있습니다. 또한 복잡도의 경우 n이 d보다 작을 경우(가장 일반적인 경우), 재귀 계층보다 더 작은 복잡도를 보입니다. n이 커지면(=sequence가 길어지면) 그 반대가 되는데, 이 때는 범위 r 만큼의 이웃들만 연산에 포함시키는 방법을 사용하여 복잡도를 줄일 수 있습니다(대신 최대 경로 길이가 상수보다 커지게 된다는 단점이 있습니다).
5. Training
5.1. Training Data and Batching
- Standard WMT 2014 English-German
- WMT 2014 English-French
- Batch size : 25000 source tokens & 25000 target tokens.
5.2. Hardware and Schedule
- GPU : 8 NVIDIA P100
- steps : 100,000 steps
- time : 12 hours
5.3. Optimizer
Adam optimizer($\beta_1 = 0.9, \beta_2 = 0.98, \epsilon = 10^{−9}$)를 사용하였습니다. 학습률은 아래 식에 따라 학습이 진행되면서 변하도록 설정했습니다.
$\text{lrate} = d_{\text{model}}^{-0.5} \cdot \min\left(\text{step_num}^{-0.5},\ \text{step_num} \cdot \text{warmup_steps}^{-1.5} \right) \quad (3)$
학습률은 warmup_steps(=4000) 동안에는 증가하다가, 다시 서서히 감소하게 됩니다.
5.4. Regularization
세 가지 regularization을 사용합니다.
- Residual Dropout 1 : 하위 계층의 출력값이 다음 하위 계층에 더해지고 정규화를 수행하기 전에 적용합니다. ($P_{drop} = 0.1$)
- Residual Dropout 2 : positional encoding과 embedding을 더할 때도 적용합니다. ($P_{drop} = 0.1$)
- Label Smoothing : $\epsilon_{ls}=0.1$, 모델의 과적합을 방지합니다.
6. Results
6.1. Machine Translation
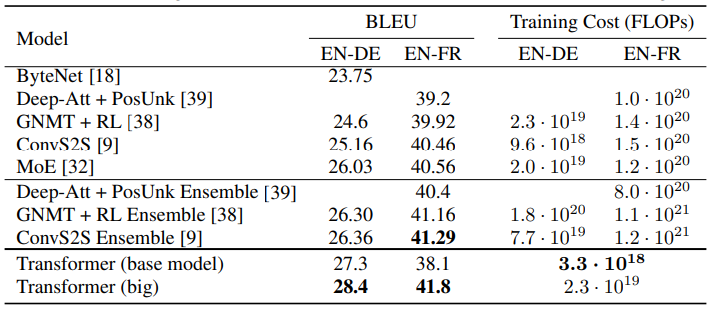
6.2. Model Variations
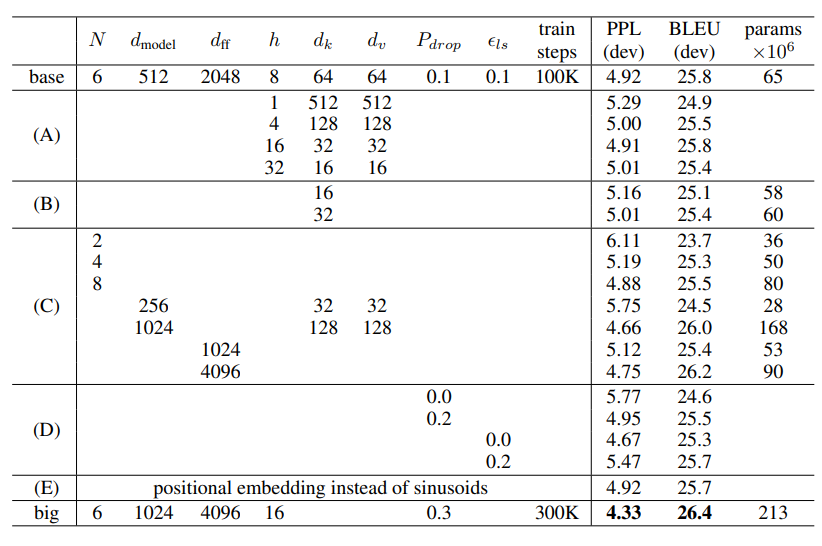
6.3. English Constituency Parsing
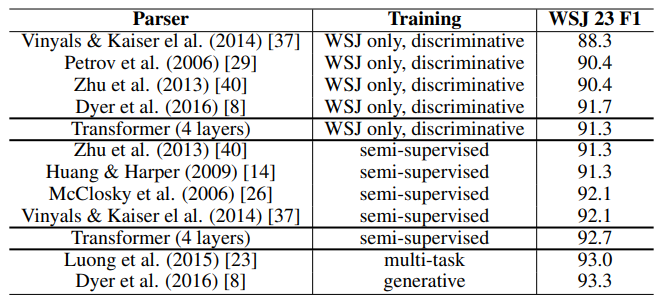
7. Conclusion
본 연구는 온전히 attention으로만 구성된 sequence 변환 모델 Transformer를 소개했습니다. Transformer는 많이 쓰이던 재귀 계층 대신 encoder-decoder 구조와 multi-head self-attention을 사용했습니다.
그 결과 번역 작업에서 Transformer는 기존의 모델보다 더 빠르게 학습하고, 새로운 SoTA 성능을 보였습니다. 앞으로 Transformer는 질의 처리까지 작업 범위를 확장하거나, 긴 sequence를 처리하기 위해 지역적으로 제한된 attention 매커니즘을 더 연구하는 등의 방향성을 잡을 수 있을 것입니다.
✅ 요약
- Encoder : 입력 sequence 전체를 self-attention으로 참조
- Decoder : 출력할 sequence를 실시간으로 참조
- Self-Attention : 각 위치가 sequence 내에서의 맥락까지 포함한 벡터값으로 바뀜
- Corss-Attention : decoder의 값과 encdoer의 값을 모두 참조 (decoder가 sequence 생성할 때 encoder를 통해 입력 sequence 전체를 참조함)
- Multi-head Attention : 일반 embedding 벡터를 Q K V 값에 맞는 차원으로 변환할 때, 가중치를 바꿔가며 head에 따른 variation을 여러 개 생성