문제
당신은 공룡이 살아 숨쉬는, N개의 섬으로 이루어진 섬나라를 여행하게 되었다. 각 섬은 1번부터 N번까지 번호가 매겨져 있으며, 당신은 이 모든 섬을 빠짐없이 방문하려고 한다.
섬들 중 어떤 M개의 쌍에는 선후 관계가 존재한다. 섬 a에서 섬 로 선후 관계가 존재한다면 반드시 a번 섬을 먼저 방문한 뒤에 섬 b를 방문해야 한다.
각 섬에는 , 로 표시되는 두 종류 중 하나의 자외선 위험이 있다. 자외선으로부터 몸을 보호하기 위해 당신은 방호복을 입어야 한다. 같은 종류의 자외선 위험이 있는 섬을 연속으로 방문하는 경우에는 방호복을 갈아 입을 필요가 없지만, 한 종류의 자외선 위험이 있는 섬을 방문한 직후에 다른 종류의 자외선 위험이 있는 섬을 방문하려면 방호복을 갈아 입어야 한다.
처음 방호복을 입을 때에는 비용이 들지 않지만, 갈아입을 때마다 1의 비용이 든다.
모든 섬을 방문하는 데 드는 최소 비용을 계산하는 프로그램을 작성하라.
예시
Example 1.
입력
5 4
0 0 1 1 0
3 2
2 4
2 5
4 1
출력
3
Example 2.
입력
4 0
1 1 1 1
출력
0
조건
- 첫 줄에 섬의 개수를 나타내는 정수 N과 선후 관계의 개수를 나타내는 정수 이 공백으로 구분되어 주어진다. (2≤N≤200 000 0≤M≤400 000)
- 그다음 줄에 각 섬의 자외선 위험 종류가 섬 번호 순서대로 공백으로 구분되어 주어진다. 자외선 위험 종류는 0 또는 로 표현된다.
- 그다음 M개의 줄에 섬들의 선후 관계들이 섬 번호의 쌍으로 주어진다. 각 줄에는 두 정수 , 가 공백으로 구분되어 주어지며, 이는 a번 섬을 먼저 방문한 다음 번 섬으로 갈 수 있음을 뜻한다. (1≤a,b≤N; a≠b)
- 같은 선후 관계는 두 번 이상 주어지지 않으며, 항상 주어진 선후 관계를 모두 만족하면서 모든 섬을 여행하는 것이 가능한 입력만 주어진다.
답
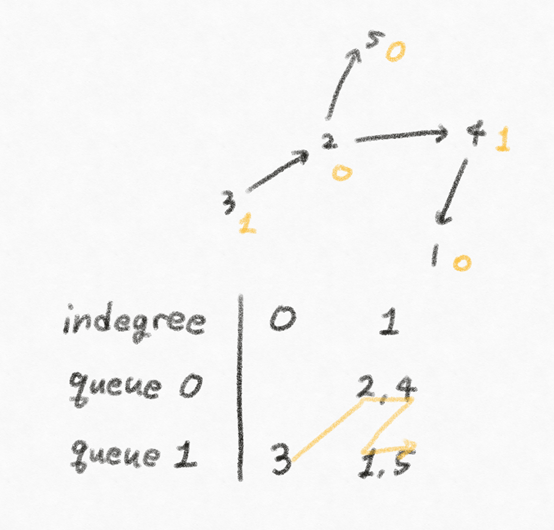
목표는 서로 다른 상태(0 or 1)의 섬을 오갈 때 드는 비용을 최소화하는 것이기 때문에,
더 이상 진행할수 없을 때 까지 한 가지 상태의 섬들을 방문하다 다른 상태의 섬으로 이동하는 방식을 사용해야 합니다.
이를 위해서는 상태 0인 섬들과 상태 1인 섬들을 분리하여 서로 다른 queue로 관리해야 합니다.
또한 의존관계가 있는 섬의 경우 이전 섬들을 방문하지 않으면 진행할 수 없기 때문에,
각 섬마다 indegree(들어오는 edge의 개수)를 세어야 합니다.
indegree가 0이 되는 섬이 나올 때 마다 queue에 집어넣어주면 됩니다.
시작하는 경우가 두 가지인데(상태 0인 섬에서 시작할 때 & 상태 1인 섬에서 시작할 때),
두 가지 경우에 대해 모두 탐색하여 둘 중 더 작은 값을 가진 쪽을 선택합니다.
// input
// N : number of islands
// M : number of relations
// A[1 - N] : UV type
// R[1 - M][0 - 1] : relation between two islands
// output
// result (number) : minimum converting cost
export const ps = (data) => {
const N = data[0][0];
const M = data[0][1];
const A = data[1];
const rels = data.slice(2);
const islands = {}
const queue0 = [], queue1 = [];
let res = N;
for (let i=1; i<=N; ++i) {
islands[i] = {
indegree: 0,
suc: [],
}
}
rels.map(rel => {
islands[rel[1]].indegree += 1;
islands[rel[0]].suc.push(rel[1]);
});
for (let i=1; i<=N; ++i) {
if (!islands[i].indegree) {
if (A[i-1]) queue1.push(i);
else queue0.push(i);
}
}
const search = (q0, q1) => {
let q = q0;
let cost = 0;
while (q0.length + q1.length > 0) {
if (q.length === 0) {
q = (q === q0)? q1 : q0;
cost++;
}
const island = q.shift();
for (const suc of islands[island].suc) {
islands[suc].indegree -= 1;
if (islands[suc].indegree === 0){
if (A[suc-1] === A[island-1]) q.push(suc);
else ((q === q0)? q1 : q0).push(suc);
}
}
}
rels.map(rel => { islands[rel[1]].indegree += 1; });
return cost
}
res = Math.min(search([...queue0], [...queue1]), search([...queue1], [...queue0]));
return res;
}시간 복잡도: O(N+M)
'CS > PS' 카테고리의 다른 글
| [PS] NYPC | 2513. 등차수열 (0) | 2025.09.17 |
|---|---|
| [PS] Leet | 155. 최솟값 스택 (0) | 2025.08.19 |
| [PS] Leet | 146. LRU 캐시 (1) | 2025.08.18 |
| [PS] Leet | 295. 데이터 스트림에서 중간값 찾기 (2) | 2025.08.06 |
| [PS] Leet | 212. 단어 찾기 II (2) | 2025.07.25 |