[review] NeRF: Representing Scene as Neural Radiance Fields for View Synthesis

2020 ECCV에 투고된 논문입니다.

https://www.matthewtancik.com/nerf?utm_source=chatgpt.com

NeRF: Neural Radiance Fields

1. Introduction

 본 연구에서는 장면 합성에서의 가장 고질적인 문제를 장면의 5차원 표현을 통해 매개변수를 직접 최적화하는 방법으로 해결했습니다. 이를 통해 입력된 이미지들과 실제 생성한 랜더링 사이의 오차를 최소화 할 수 있었습니다.

 

 여기서 말하는 5차원 표현은 특정 지점(x, y, z)에서의 시점 방향(θ, φ)으로 이루어져 있습니다. 여기에 추가로 해당 지점에서 광선의 빛을 얼마나 흡수 하느냐(=얼마나 불투명해지는가 =물체가 있을 확률이 높은가)도 판단합니다. NeRF는 이 5차원 좌표(x, y, z, θ, φ)와 그에 따른 부피밀도(volume density) 및 색상(RGB) 사이의 회귀분석을 통해 MLP 신경망을 최적화합니다.

 

[그림 1]

 Neoural Radiance Field(NeRF) 랜더링은 다음과 같은 과정을 거칩니다.

1. 카메라에서 물체를 관통하는 광선을 쏘아 거기게 속하는 3D point들을 생성
2. 이 point 그룹과 광선 방향을 입력값으로 하여 인공신경망을 통해 각 point의 색상과 밀도를 출력
3. 생성한 색상과 밀도들을 누적하여 최종적으로 2D 이미지를 생성

 이 전 과정은 미분 가능하기 때문에, 경사하강법을 이용하여 최적화가 가능합니다. 이 때 에러의 기준은 각 시점에서 본 원래 이미지와 NeRF가 해당 시점에서 생성한 이미지 사이의 차이가 됩니다. 전체적인 pipeline은 [그림 2]에 제시되어 있습니다.

[그림 2] NeRF의 장면 생성과 랜더링 절차

 또 한가지, NeRF는 복잡한 장면에 대해서 고해상도 생성이 어렵고 비효율적이다는 단점이 있었습니다. 하나의 광선에 대해 추출해야 하는 샘플의 수가 많기 때문입니다. 이를 해결하기 위해 5차원의 입력 좌표를 바로 넣는 것이 아니라, positional encoding을 통해 high-frequency 정보를 학습할 수 있게 하였습니다. 또한 계층적 샘플링을 도입하여 충분한 데이터가 모인 부분(= 덜 복잡한 부분)은 샘플링을 덜 하도록 설계했습니다.

 

  NeRF는 복잡한 구조와 외형을 잘 표현할 수 있으며, 그래디언트 기반의 최적화가 가능하다는 volumetric representation의 이점을 가지고 있습니다. 또한, 고해상도의 장면을 저장할 때 많은 양의 저장용량이 필요햔 voxel grid 기법의 문제점 또한 해결 할 수 있습니다.

 

 본 연구는 RGB 장면 이미지들이 주어졌을 때 처음으로 고해상도의 새로운 장면을 만들어내는데 성공한 continuous neural scene representation 기법이라고 할 수 있습니다.

2. Related work

- Neural 3D shape representations

- View synthesis and image-based rendering

3. Neural Radiance Field Scene Representation

 NeRF의 인공신경망은 입력값이 3차원 위치 x(x, y, z)와 2차원 방향 (θ, φ)으로 총 5차원이며, 출력값은 3차원 색상 c(r, g, b)와 부피 밀도 σ입니다. 여기서 2차원 방향을 3D Cartesian univector d로 나타낸다면, 가중치를 Θ로 하는 MLP 인공신경망을 다음과 같이 나타낼 수 있습니다.

$F_{\Theta} : (x, d) \rightarrow (c, \sigma)$

 

 본 연구에서는 결과 모습이 장면과 관계없이 일관적이게 하기 위해 부피 밀도 σ를 위치 x(x, y, z)값에 대한 함수로만 표현되도록 했습니다. 어느 위치에서 보더라도(=시점 방향), 특정 지점에서의 물체의 밀도는 변하지 않아야 하기 때문입니다. 이를 위해 입력값은 두 차례의 신경망을 통과합니다.

1. x(x, y, z)가 8개의 완전연결층을 통과합니다.
2. 출력값은 시점 방향에 의존적이지 않은 부피 밀도 σ와 256차원의 feature vector를 내놓게 됩니다.
3. feature vector는 시점방향 d와 합쳐져 하나의 완전연결층을 통과합니다.
4. 출력값은 시점 방향에 의존적인 색상 c(r, g, b)를 내놓게 됩니다.

[그림 3] 시점에 따라 달라지는 색상

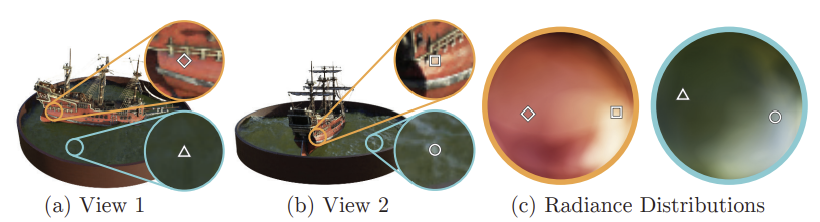
 [그림 4]에서 볼 수 있듯, 시점 의존성을 반영하지 않고 모델을 학습시키면 specularity가 제대로 반영되지 않음을 알 수 있습니다.

[그림 4] View dependency와 positional encoding에 따른 랜더링 결과

4. Volume Rendering with Radiance Fields

 NeRF가 생성한 부피 밀도 σ를 통해 랜더링을 수행할 때는 기존에 사용하던 부피 랜더링 방식을 사용합니다. 위치 x(x, y, z)에 대해 나타나는 부피 밀도 함수 σ(x)는 어떤 광선이 일직선으로 진행하다가 정지할 확률을 나타내는 확률 함수로 볼 수 있습니다. 따라서 어떤 카메라 광선 $r(t) = o + td$가 있을 때, t의 구간 [$t_n$, $t_f$]에서의 예상 색상값 $C(r)$은 다음과 같이 나타낼 수 있습니다. 여기서 $T(t)$는 누적 투과율로 $t_n$에서 $t$까지 광선이 막히지 않고 지나올 확률을 나타냅니다.

 

$C(\mathbf{r}) = \int_{t_n}^{t_f} T(t) \, \sigma(\mathbf{r}(t)) \, \mathbf{c}(\mathbf{r}(t), \mathbf{d}) \, dt, \quad \text{where} \quad T(t) = \exp\left(-\int_{t_n}^{t} \sigma(\mathbf{r}(s)) \, ds\right)$

 

 위 적분과정은 구간 내 몇몇 값들을 골라 계산해내는 수치적(quadrature)인 방식으로 진행됩니다. 단, 기존 voxel grids에서 사용되던 deterministic quadrature 방식은 고정된 소수의 위치만 선택되어 제약이 있기에 다른 방식인 stratified sampling 방식을 사용합니다. 이는 구간 [$t_n$, $t_f$]을 N등분 하여 각 구간에서 uniform 분포에 따라 샘플을 하나씩 선택하는 방법입니다.

 

$t_i \sim \mathcal{U} \left[ t_n + \frac{i - 1}{N} (t_f - t_n),\; t_n + \frac{i}{N} (t_f - t_n) \right]$

 

 이렇게 하면 고정된 위치에서만 MLP를 실행하지 않고, 무작위 연속적인 값에 대해 실행할 수 있습니다. 그리하여 위의 C(r)에 대한 적분식은 다시 아래와 같은 이산적인 형태로 나타낼 수 있습니다.

 

$\hat{C}(\mathbf{r}) = \sum_{i=1}^{N} T_i \left(1 - \exp(-\sigma_i \delta_i)\right) \mathbf{c}_i, \quad \text{where} \quad T_i = \exp\left( - \sum_{j=1}^{i-1} \sigma_j \delta_j \right)$

 

※ $\delta_i = t_{i+1} - t_i$

5. Optimizing a Neural Radiance Field

 위에서 언급했던 요소들은 장편 합성을 위해 기본적으로 필요한 단계에 해당합니다. 이것만으로는 SotA 성능을 발휘하기 어렵기 때문에, 본 연구에서는 positional encoding과 hierarchical sampling이라는 두 가지 개념을 도입하였습니다.

5.1. Positional encoding

 인공신경망 $F_\Theta$가 5차원 입력값(x, y, z, θ, φ)을 바로 받으면 high-frequency 정보를 제대로 반영할 수 없습니다. 대부분 신경망의 경우 lower_frequency정보에 편향되어 학습되는 경향이 있기 때문입니다. 입력값을 더 높은 차원의 공간으로 변형한다면 high-frequency 정보도 반영될 수 있습니다.

 

 본 연구에서는 이 특징을 활용하여 기존의 인공신경망을 두 개의 함수로 분리하여 $F_\Theta = F^{\prime}_{\Theta} \circ \gamma$로 나타냅니다. $\gamma$는 높은 차원 공간으로 변형하는 $\mathbb{R} \rightarrow \mathbb{R}^{2L}$ 함수이고, $ F^{\prime}_{\Theta}$는 일반적인 MLP입니다. $\gamma$를 조금 더 자세히 전개하면 다음과 같습니다.

 

$\gamma(p) = \left( \sin(2^0 \pi p), \cos(2^0 \pi p), \cdots, \sin(2^{L-1} \pi p), \cos(2^{L-1} \pi p) \right)$

 

 $\gamma$는 입력값의 개별 요소(위치 x의 x, y, z와 시점 방향 d의 unit vector 요소들)에 각각 적용됩니다. 본 연구는$\gamma(x)$에서 L=10, $\gamma(d)$에서 L=4 로 설정했습니다.

 

 비슷한 방식의 매핑 함수가 Transformer 구조에서도 사용됩니다. 그곳에서는 positional encoding으로 불리는데, 그 목적은 조금 다릅니다. Transformer는 순서를 알 수 없는 토큰 구조에 순서를 부여하기 위해서 사용하지만, 본 연구에서는 좌표 정보를 높은 차원 공간으로 매핑하여 high-frequency 정보를 부여하기 위함입니다.

5.2. Hierarchical volume sampling

 지금의 랜더링 방식은 비어 있거나 가려져 보이지 않더라도 카메라 광선을 따라 샘플링되는 지점이 존재해 상당히 비효율적입니다. 따라서 표현될 지점이 많을 것으로 예상되는 지점에는 샘플링 지점의 개수를 늘리는 hierarchical sampling을 적용하였습니다.

 

 본 연구에서는 이를 구현하기 위해 'fine'과 'coarse' 두 개의 신경망을 최적화에 사용했습니다. 먼저 각 광선에 대해 stratified sampling으로 $N_c$개의 구간을 선정한 후, 각 위치에 대해 coarse 신경망을 실행합니다(4절 참고).

 

$t_i \sim \mathcal{U} \left[ t_n + \frac{i - 1}{N} (t_f - t_n),\; t_n + \frac{i}{N} (t_f - t_n) \right]$

 

 이 때 C(r)을 $N_c$개의 구간에 대해 아래와 같이 바꿔 씁니다.

 

$\hat{C_c}(\mathbf{r}) = \sum_{i=1}^{N_c} w_i c_i,  \quad \text{where} \quad  w_i = T_i \left(1 - \exp(-\sigma_i \delta_i)\right)$

 

 여기서 치환한 가중치 $w_i$를 정규화하면, $N_c$의 각 구간 내에서는 일정한 값을 가지기 때문에 광선을 따라 분포하는 계단 모양의 확률밀도함수를 얻을 수 있습니다.

 

$\hat{w}_i = w_i / \sum_{j=1}^{N_c} w_j$

 

 두 번째 $N_f$개의 구간은 위의 확률밀도함수를 통해 선택됩니다. 이렇게 coarse와 fine 구간 두 가지를 모두 선택했다면 두 가지를 모두 합쳐 fine 신경망을 실행합니다. 마지막 랜더링 과정에서 색상값 $\hat{C}_f(r)$을 구할 때도 $N_c + N_f$개의 구간을 모두 사용합니다. 이렇게 하면 화면에 보이는 지점을 더 많이 찾을 수 있습니다.

5.3. Implementation details

 

6. Results

 

7. Conclusion